Fragestellungen
Über diese Applikation
- Diese Webapplikation ist ein Demonstrator zu Forschungszwecken. Die Entwicklung wurde zum Ende der Projektlaufzeit am 30.06.2022 eingestellt. Interne Parameter für die Modellierung der Fragestellungen basieren auf Ergebnissen einer Literaturrecherche, die zuletzt am 03.02.2022 geupdatet wurde. Das Infektionsgeschehen kann sich aber weiterhin ändern. Die Korrektheit der Auswertungen wird daher nicht garantiert!
- Sie dient der statistischen Abschätzung weiterer Coronafälle und kann damit den Gesundheitsämtern für bestimmte Fragestellungen als Entscheidungshilfe dienen.
- Zur Auswertung dürfen nur anonymisierte Daten hochgeladen werden.
Entwicklung & Forschung
Diese Applikation wird entwickelt von
- Fraunhofer Institut für Techno- und Wirtschaftsmathematik ITWM
- Fraunhofer Institut für Digitale Medizin MEVIS
- Leibniz Institut für Präventionsforschung und Epidemiologie BIPS
- in Zusammenarbeit mit Dr. Jakob Schumacher vom Gesundheitsamt Berlin-Reinickendorf.
- Das Forschungsvorhaben wurde vom 15.05.2020 - 14.12.2020 innerhalb des Fraunhofer Anti-Corona-Programms und vom 01.07.2021 - 30.06.2022 innerhalb des Programms Prävention und Versorgung epidemisch auftretender Infektionen mit innovativer Medizintechnik vom Bundesministerium für Bildung und Forschung gefördert.
Impressum
Das Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM
Fraunhofer-Platz 1, 67663 Kaiserslautern
ist eine rechtlich nicht selbstständige Einrichtung der
Fraunhofer-Gesellschaft zur Förderung der angewandten Forschung e.V.Hansastraße 27c, 80686 München
Telefon +49 89 1205- 0
Fax +49 89 1205-7531
E-Mail: info(at)zv.fraunhofer.de
Umsatzsteuer-Identifikationsnummer gemäß § 27a Umsatzsteuergesetz
DE 129515865
Registergericht
Amtsgericht MünchenEingetragener Verein
Register-Nr. VR 4461
Redaktionsverantwortlich im Sinne des Presserechts
Kontakt: Dr. Stefanie Grimm
Vorstand
Dr. Sandra Krey | Mitglied des Vorstands | führt die Fraunhofer-Gesellschaft interimistischProf. Dr. Alexander Kurz | Mitglied des Vorstands
Prof. Dr. Axel Müller-Groeling | Mitglied des Vorstands
Ass. jur. Elisabeth Ewen | Mitglied des Vorstands
Nutzungsrechte
Copyright © byFraunhofer-Gesellschaft
Alle Rechte vorbehalten.Die Urheberrechte dieser Web-Site liegen vollständig bei der Fraunhofer-Gesellschaft.
Ein Download oder Ausdruck dieser Veröffentlichungen ist ausschließlich für den persönlichen Gebrauch gestattet. Alle darüber hinaus gehenden Verwendungen, insbesondere die kommerzielle Nutzung und Verbreitung, sind grundsätzlich nicht gestattet und bedürfen der schriftlichen Genehmigung.
Anfragen richten Sie bitte an:
Fraunhofer-Institut für Techno- und WirtschaftsmathematikFraunhofer-Platz 1, 67663 Kaiserslautern
Ein Download oder Ausdruck ist darüber hinaus lediglich zum Zweck der Berichterstattung über die Fraunhofer-Gesellschaft und Ihre Institute nach Maßgabe unten stehender Nutzungsbedingungen gestattet.
Grafische Veränderungen an Bildmotiven - außer zum Freistellen des Hauptmotivs - sind nicht gestattet. Es ist stets die Quellenangabe und Übersendung von zwei kostenlosen Belegexemplaren an die oben genannte Adresse erforderlich. Die Verwendung ist honorarfrei.
Haftungshinweis
Wir übernehmen keine Haftung für die Inhalte externer Links. Für den Inhalt der verlinkten Seiten sind ausschließlich deren Betreiber verantwortlich.
Wir sind bemüht, das Webangebot stets aktuell und inhaltlich richtig sowie vollständig anzubieten. Dennoch ist das Auftreten von Fehlern nicht völlig auszuschließen. Das Fraunhofer-Institut bzw. die Fraunhofer-Gesellschaft übernimmt keine Haftung für die Aktualität, die inhaltliche Richtigkeit sowie für die Vollständigkeit der in ihrem Webangebot eingestellten Informationen. Dies bezieht sich auf eventuelle Schäden materieller oder ideeller Art Dritter, die durch die Nutzung dieses Webangebotes verursacht wurden.
Geschützte Marken und Namen, Bilder und Texte werden auf unseren Seiten in der Regel nicht als solche kenntlich gemacht. Das Fehlen einer solchen Kennzeichnung bedeutet jedoch nicht, dass es sich um einen freien Namen, ein freies Bild oder einen freien Text im Sinne des Markenzeichenrechts handelt.
Datenschutz
Alle Informationen zum Datenschutz finden Sie in unserer Datenschutzerklärung und auf der Datenschutzseite zu shinyapps.io. In dieser Webapplikation werden keine Daten dauerhaft gespeichert.
Fragestellung
Eine Gruppe hat sich getroffen und nacheinander erkranken Personen. Wie viele Erkrankungen sind wahrscheinlich in den nächsten Tagen noch zu erwarten?
Dateneingabe
Für die Analyse werden Informationen über die Gruppe (1. Schritt) sowie bekannte Informationen zu erkrankten Gruppenmitgliedern (2. Schritt) benötigt.
Schritt 1 von 2: Eingabe der Gruppendaten
Geben Sie zunächst die Gruppengröße (inklusive aller Erkrankten und Nicht-Erkrankten) sowie das Datum des Kontaktereignisses ein.
Hinweis: Falls ein oder mehrere Indexfälle bekannt sind, die bereits vor dem Event infiziert waren, so schließen Sie diese bitte aus Ihren Angaben aus!
Schritt 2 von 2: Eingabe der Erkrankungsdaten
Geben Sie nun die Symptombeginndaten inklusiver der Anzahl der an dem Tag neu erkrankten Personen ein.
Antwort
oo
oo
Grafische Darstellung
Wissenschaftliche Grundlagen [Stand 30.06.2022]
Die zugrundeliegenden Parameter für die Modellierung stammen aus
Xin et al. (2021). The Incubation Period Distribution of Coronavirus Disease 2019: A Systematic Review and Meta-Analysis. Clinical Infectious Diseases.
Die Wahl für diese Quelle erfolgte als Ergebnis der Literaturrecherche aus
Kühne et al. (2022). EsteR - Decision support for German health authorities by risk modelling in order to contain the COVID-19 pandemic. Protocol for a rapid review. OSF Preprints.
Fragestellung
Eine Gruppe hat sich getroffen und mindestens eine Person davon war infiziert. Nach dem Kontaktereignis wurden Tests von einem Teil der Gruppe durchgeführt und alle Testergebnisse sind negativ ausgefallen. Wie wahrscheinlich ist es, dass niemand infiziert wurde und keine weiteren Coronafälle auftreten?
Dateneingabe
Für die Analyse werden Informationen über die Gruppe (1. Schritt) sowie Informationen zu negativ getesteten Gruppenmitgliedern (2. Schritt) benötigt.
Schritt 1 von 2: Eingabe der Gruppendaten
Geben Sie zunächst die Gruppengröße (inklusive aller Erkrankten und Nicht-Erkrankten), die Anzahl an bereits erkrankten Fällen sowie Informationen zum Kontaktereignis ein.
Eingegebenes Kontaktereignisdaten:
Schritt 2 von 2: Eingabe von negativen Testergebnissen
Geben Sie nun für jede Testgruppe nacheinander die Informationen zu Testdatum und -art ein.
Nach Eingabe der Daten einer Testgruppe muss auf
Hinzufügen
geklickt werden, um die Daten in die Berechnung einfließen zu lassen.
Hinweis: Eine Testgruppe besteht aus Personen, die alle negativen Tests an gleichen Tagen und mit der gleichen Testart durchgeführt haben.
Eingegebene negative Testergebnisse:
oo Testzeitpunkte ooooooooooooo Anzahl
Nach Prüfung der Eingaben kann die Antwort berechnet werden:
Antwort
Zeitlicher Verlauf der eingegebenen Daten
Wissenschaftliche Grundlagen [Stand 30.06.2022]
Die zugrundeliegenden Parameter für die Modellierung stammen aus
Schoeps et al. (2021). Surveillance of SARS-CoV-2 transmission in educational institutions, August to December 2020, Germany. Epidemiology and Infection.
Das statistische Modell wird in folgendem publizierten Journalpaper genauer erklärt:
Jäckle et al. (2021). Statistical Model to Assess Risk for Supporting COVID-19 Quarantine Decisions. International Journal of Environmental Research and Public Health.
Fragestellung
Eine Person / Gruppe hat sich mit Corona infiziert. Wann geschah die Infektion mit Corona? Geben sie dazu den Symptombeginn der erkrankten Personen ein.
Dateneingabe
Antwort
oo
Grafische Darstellung
Wissenschaftliche Grundlagen [Stand 30.06.2022]
Die zugrundeliegenden Parameter für die Modellierung stammen aus
Xin et al. (2021). The Incubation Period Distribution of Coronavirus Disease 2019: A Systematic Review and Meta-Analysis. Clinical Infectious Diseases.
Die Wahl für diese Quelle erfolgte als Ergebnis der Literaturrecherche aus
Kühne et al. (2022). EsteR - Decision support for German health authorities by risk modelling in order to contain the COVID-19 pandemic. Protocol for a rapid review. OSF Preprints.
Fragestellung
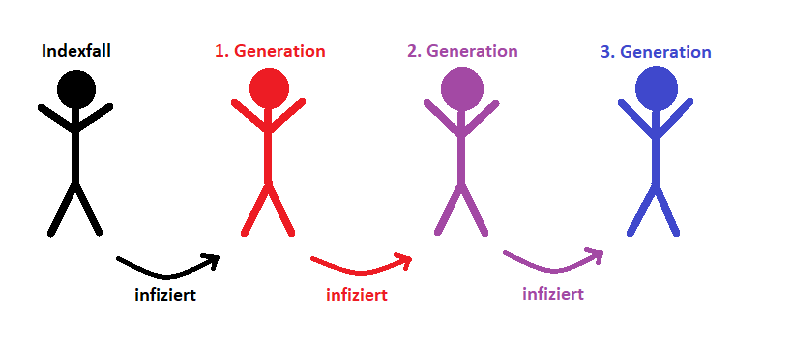
Eine Person hat sich mit Corona infiziert. Wann werden erkrankte Kontaktpersonen erste Symptome zeigen? Geben sie dazu den Symptombeginn der erkrankten Person ein.
Dateneingabe
Antwort
oo Kontakte 1. Generation
oo
oo Kontakte 2. Generation
oo
oo Kontakte 3. Generation
oo
Grafische Darstellung
Wissenschaftliche Grundlagen [Stand 30.06.2022]
Die zugrundeliegenden Parameter für die Modellierung stammen aus
Son et al. (2020). Epidemiological characteristics of and containment measures for COVID-19 in Busan, Korea. Epidemiology and Health.
Die Wahl für diese Quelle erfolgte als Ergebnis der Literaturrecherche aus
Kühne et al. (2022). EsteR - Decision support for German health authorities by risk modelling in order to contain the COVID-19 pandemic. Protocol for a rapid review. OSF Preprints.
Fragestellung
Eine Person hat sich mit Corona infiziert. Wann war die Person ansteckend? Geben sie dazu an, ob die Person Symptome hat oder nicht, und geben sie anschließend die weiteren benötigten Daten ein.
Dateneingabe
Antwort
oo
Grafische Darstellung
Wissenschaftliche Grundlagen [Stand 30.06.2022]
Die zugrundeliegenden Parameter für die Modellierung bei bekanntem Symptombeginndatum stammen aus
He et al. (2020). Temporal dynamics in viral shedding and transmissibility of COVID-19. Nature Medicine.
Für den Fall ohne bekannten Symptombeginn bilden wir die Empfehlungen des RKI ab:
Robert Koch-Institute. Kontaktpersonen-Nachverfolgung (KP-N) bei SARS-CoV-2-Infektionen.